Turbulente Strömung
| Der hydraulische Durchmesser dH wird so gewählt, dass Druckverlust und mittlere Strömungsgeschwindigkeit im vollständig gefüllten runden Rohr mit dH und im nicht kreisförmigen Querschnitt gleich sind. Der Volumenstrom muss umgerechnet werden. | ||||||||||||||
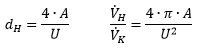 | A: durchströmte, nicht kreisförmige Querschnittsfläche U: durchströmter, nicht kreisförmiger Umfang | |||||||||||||
| rechteckiger Kanal: | ||||||||||||||
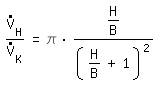 |  : Volumenstrom im Rohr mit dH : Volumenstrom im Rohr mit dH : Volumenstrom im rechteckigen Kanal : Volumenstrom im rechteckigen KanalH : Kanalhöhe B : Kanalbreite | |||||||||||||
| ||||||||||||||
Laminare Strömung
| Der hydraulische Durchmesser dH kann für ausgewählte Querschnitte so bestimmt werden, dass Druckverlust und Volumenstrom im vollständig gefüllten runden Rohr mit dH und im nicht kreisförmigen Querschnitt gleich sind. | ||||||||||||||
| rechteckiger Kanal: | ||||||||||||||
| dH = H · f (H/B) | H: Kanalhöhe B: Kanalbreite, B > H f(H/B): Herleitung siehe unten | |||||||||||||
| ||||||||||||||
Theorie
Turbulente StrömungBei turbulenter Strömung wählt man den hydraulischen Durchmesser des Ersatzrohres so, dass Wandschubspannung τw und Druckverlust Δp des Ersatzrohres der mittleren Wandschubspannung und dem Druckverlust des nicht kreisförmigen Kanals gleichen. Damit gilt für die Kräftegleichgewichte des Ersatzrohres und des nicht kreisförmigen Kanals:
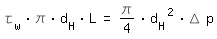 |
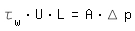 |
L : Länge |
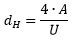 | ||
Bei gleicher mittlerer Strömungsgeschwindigkeit baut sich im vollständig gefüllten Rohr mit hydraulischem Durchmesser dH der gleiche Druckabfall auf wie im nicht kreisförmigen Querschnitt. Das Verhältnis von mittlerer Wandschubspannung zu mittlerer Strömungsgeschwindigkeit ist in beiden Systemen näherungsweise gleich, da die Geschwindigkeitsverteilung bei turbulenter Strömung sehr flach ist.
Die Volumenströme müssen umgerechnet werden. Mit gleicher mittlerer Geschwindigkeit erhält man:
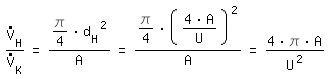
rechteckiger Kanal:
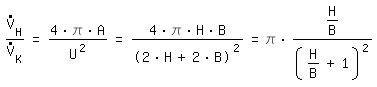
Laminar Strömung Bei laminarer Strömung existieren für zahlreiche Querschnitte gute Näherungsformeln für den Volumenstrom als Funktion des Druckverlustes. [Berker 1963] resümiert geschlossene Lösungen der Geschwindigkeitsverteilungen laminarer Strömung in diversen Querschnitten.
Für einen Rechteckkanal mit den Abmessungen BxH gilt mit B>H:
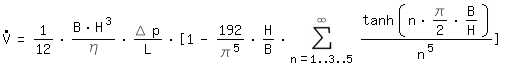
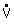 : Volumenstrom
η: dynamische Viskosität
L: Kanallänge
: Volumenstrom
η: dynamische Viskosität
L: KanallängeFür B>>H konvergiert diese Gleichung gegen die Lösung für zwei parallele Platten, auch Couette Strömung genannt (Herleitung s. Anhang):
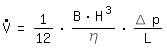
Den hydraulischen Durchmesser gewinnt man wie folgt:
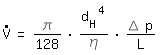 |
laminare Rohrströmung (Hagen Poiseuille Strömung) (Herleitung siehe Anhang) | |
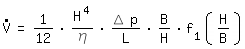 |
laminare Strömung im Rechteckkanal |
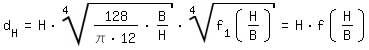
 |
| Hagen Poiseuille and Couette Flow |
| Literatur |
| [Berker 1963] Tapis Berker, Encyclopedia Of Physics / Handbuch der Physik, Edited by S. Flügge, Springer-Verlag 1963, page 70 |