Reibungsbehaftete Strömung durch gerade Rohrleitungen
| Δ p = f · l/d · ρ/2 · v2 (Darcy-Weisbach Gleichung) |
| dimensionsbehaftete Grössen (z.B. metrisch) | ||
| Δ p | [kg/(m s²) = 10-5 bar = 10-2mbar] | : Druckverlust der geraden Rohrlänge |
| l | [m] | : Länge |
| d | [m] | : Innendurchmesser |
| ρ | [kg/m³] | : Dichte |
| v | [m/s] | : mittlere Geschwindigkeit im Rohr |
| η | [kg/(m s) = Pas] | : Dyn. Viskosität |
| ε | [m] | : Rohrrauhigkeit |
| dimensionslose Grössen | ||
| Re | [-] | : Reynolds-Zahl Re = ρ v d / η |
| f | [-] | : Rohrreibungszahl |
Für Re < 2320 (laminare Rohrströmung) wird die Rohrreibungszahl nach Hagen-Poiseuille berechnet:
f = 64 / Re
 Hagen Poiseuille and Couette Flow
Hagen Poiseuille and Couette Flow
Für Re > 2320 (turbulente Rohrströmung) wird die Rohrreibungszahl
nach [Colebrook 1939, Seite 137] berechnet:
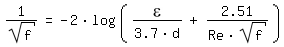
|
Die Beziehung von Colebrook konvergiert für Re => ∞ (vollständig turbulente Strömung) gegen die Beziehung von [Prandtl 1933, Seite 110] nach Kármán:
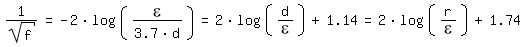
und für ε/d => 0 (glattes Rohr) gegen die Beziehung von [Prandtl 1933, Seite 111]:
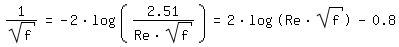
Da laminare Rohrströmung bis Re = 8000 möglich ist
[VDI 1984, Seite Lb1], kann es durch den vorgenannten Rechenweg im kritischen Bereich
(2320 <= Re < 8000) zu einer Überschätzung der Rohrreibungszahl kommen.
Das Moody-Diagramm nach [Moody 1944, Seite 672] ist eine
gelungene Darstellung vorgenannter Gleichungen.
 |
 | |
| Moody Re: 10-106 | Moody Re: 100-108 | |
Mit 1/f^0,5 = Re/200 · ε /d und 1/f^0,5 = 2log(r/ε) + 1,74 grenzt [Moody 1944, Seite 676] den Übergangsbereich vom Bereich vollständig turbulenter Rohrströmung ab.
| Literatur |
| [Colebrook 1939] C.F. Colebrook, Turbulent Flow in Pipes, with particular reference to the Transition Region between the Smooth and Rough Pipe Laws, Journal of The Institution of Civil Engineers, Volume 11, 1939 |
| [Moody 1944] L.F.Moody, Friction Factors of Pipe Flow, Transactions of the ASME, Volume 66, 1944 |
| [Prandtl 1933] L. Prandtl, Neuere Ergebnisse der Turbulenzforschung, Zeitschrift des Vereins Deutscher Ingenieure, Band 77, 1933 |
| [VDI 1984] VDI-Wärmeatlas 4. Auflage 1984 |